Esercitazione di laboratorio #1 - Controlli Automatici
Soluzione dell'esercizio riguardante il sistema meccanico
Autori: M. Indri, M. Taragna (ultima modifica: 31/03/2020)
Contents
Introduzione
Si puo' suddividere il programma in diverse sezioni di codice usando i caratteri "%%". Ogni sezione puo' essere eseguita separatamente dalle altre con il comando "Run Section" (nella toolbar dell'Editor, subito a destra del tasto "Run"). Si puo' ottenere lo stesso risultato selezionando la porzione di codice che si vuole eseguire e premendo il tasto funzione F9, risparmiando cosi' tempo rispetto all'esecuzione di tutto il programma. Si prenda questo script come esempio di riferimento.
clear all, close all, clc
Procedimento
- Definizione dei parametri del sistema e del tipo di simulazione
- Definizione della rappresentazione di stato del sistema
- Calcolo numerico dell'evoluzione di stati e uscita del sistema dinamico
- Confronto grafico dei risultati ottenuti
- Calcolo della funzione di trasferimento come oggetto "transfer function"
- Calcolo della funzione di trasferimento come come rapporto di polinomi
- Definizione della trasformata di Laplace dell'ingresso
- Calcolo della trasformata di Laplace dell'uscita
- Scomposizione in fratti semplici della trasformata di Laplace dell'uscita
Definizione del sistema dinamico
% Passo 1: definizione dei parametri del sistema e del tipo di simulazione es=menu('Simulazione della risposta del sistema meccanico',... 'caso 1.a: beta=0.1, K=2, x0=[0;0], F(t)=1;',... 'caso 1.b: beta=0.01, K=2, x0=[0;0], F(t)=1;',... 'caso 1.c: beta=10, K=20, x0=[0;0], F(t)=1;',... 'caso 1.d: beta=0.1, K=2, x0=[0;0.2], F(t)=1;',... 'caso 2.a: beta=0.1, K=2, x0=[0;0], F(t)=cos(4t);',... 'caso 2.b: beta=0.01, K=2, x0=[0;0], F(t)=cos(4t);',... 'caso 2.c: beta=10, K=20, x0=[0;0], F(t)=cos(4t);',... 'caso 2.d: beta=0.1, K=2, x0=[0;0.2], F(t)=cos(4t)'); switch es, case 1, beta=0.1; k=2; x0=[0;0]; w0=0; tmax=20; case 2, beta=0.01; k=2; x0=[0;0]; w0=0; tmax=200; case 3, beta=10; k=20; x0=[0;0]; w0=0; tmax=10; case 4, beta=0.1; k=2; x0=[0;0.2]; w0=0; tmax=20; case 5, beta=0.1; k=2; x0=[0;0]; w0=4; tmax=10; case 6, beta=0.01; k=2; x0=[0;0]; w0=4; tmax=10; case 7, beta=10; k=20; x0=[0;0]; w0=4; tmax=10; case 8, beta=0.1; k=2; x0=[0;0.2]; w0=4; tmax=10; end m=0.2; f0=1; % Passo 2: definizione della rappresentazione di stato del sistema A=[0, -k/m; 1, -k/beta]; B=[1/m; 0]; C=[1, 0]; D=0; sistema=ss(A,B,C,D);
Simulazione della risposta del sistema dinamico
% Passo 3: calcolo numerico dell'evoluzione di stati e uscita del sistema dinamico t=0:0.01:tmax; u=f0*cos(w0*t); [y,tsim,x]=lsim(sistema,u,t,x0); % Passo 4: confronto grafico dei risultati ottenuti figure(1), plot(tsim,x(:,1)), grid on, zoom on, title('Evoluzione dello stato x_1'), xlabel('tempo (in s)'), ylabel('velocità v (in m/s)') figure(2), plot(tsim,x(:,2)), grid on, zoom on, title('Evoluzione dello stato x_2'), xlabel('tempo (in s)'), ylabel('posizione p_A (in m)') figure(3), plot(tsim,y), grid on, zoom on, title('Evoluzione dell''uscita y'), xlabel('tempo (in s)'), ylabel('velocità v (in m/s)')
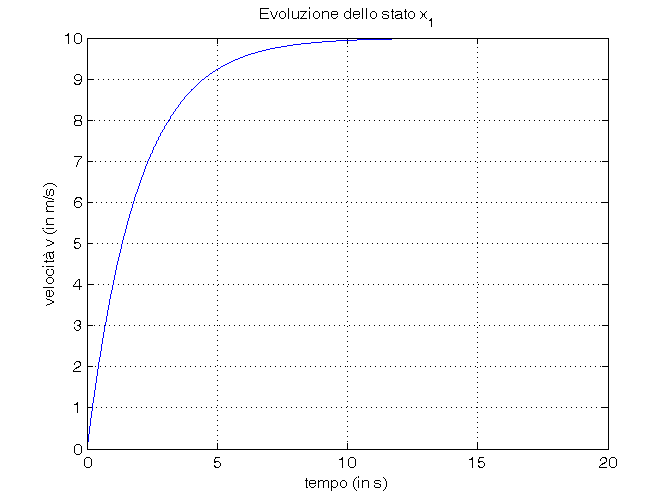
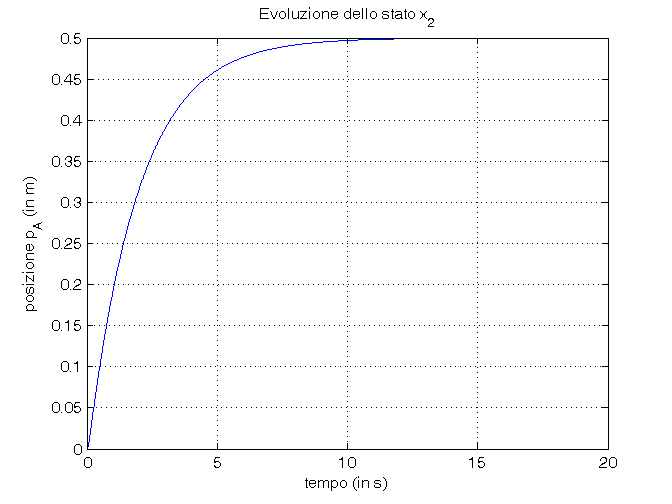
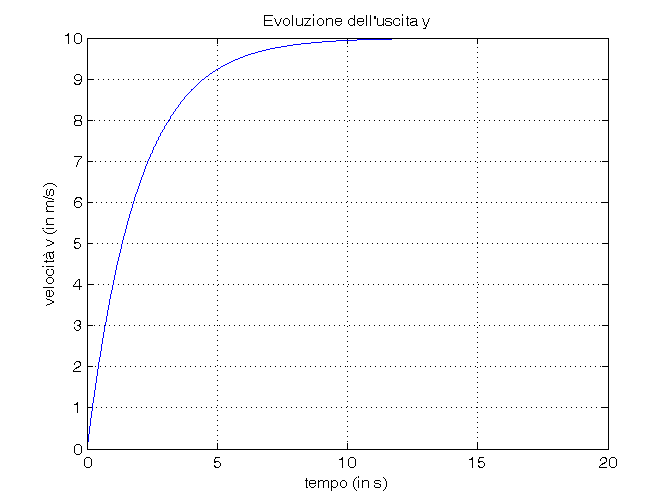
Calcolo della funzione di trasferimento del sistema dinamico
% Passo 5: calcolo di G(s) come oggetto di tipo "transfer function" fprintf('System G(s)'); G=tf(sistema) % Passo 6: calcolo di G(s) come rapporto di polinomi [numG,denG]=ss2tf(A,B,C,D) fprintf('Zeri di G(s)'); damp(numG); % Calcolo degli zeri di G(s) fprintf('Poli di G(s)'); damp(denG); % Calcolo dei poli di G(s)
System G(s)
G =
5 s + 100
---------------
s^2 + 20 s + 10
Continuous-time transfer function.
numG =
0 5 100
denG =
1.0000 20.0000 10.0000
Zeri di G(s)
Pole Damping Frequency Time Constant
(rad/TimeUnit) (TimeUnit)
-2.00e+01 1.00e+00 2.00e+01 5.00e-02
Poli di G(s)
Pole Damping Frequency Time Constant
(rad/TimeUnit) (TimeUnit)
-1.95e+01 1.00e+00 1.95e+01 5.13e-02
-5.13e-01 1.00e+00 5.13e-01 1.95e+00
Calcolo analitico di risposte nel tempo del sistema dinamico
% Passo 7: definizione della trasformata di Laplace U(s) dell'ingresso u(t) fprintf('Input U(s)'); ingresso=menu('Tipo d''ingresso del sistema','u(t)=u0;','u(t)=t;','u(t)=u0*cos(4t)'); % Soluzione #1: esplicitando i polinomi di U(s) switch ingresso, case 1, U=tf(1,[1,0]) case 2, U=tf(1,[1,0,0]) case 3, U=tf([1,0],[1,0,4^2]) end % Soluzione #2 (equivalente): introducendo l'oggetto "transfer function" s s=tf('s'); switch ingresso, case 1, U_=1/s % tf(1,[1,0]) case 2, U_=1/s^2 % tf(1,[1,0,0]) case 3, U_=s/(s^2+4^2) % tf([1,0],[1,0,4^2]) end % Passo 8: calcolo della trasformata di Laplace Y(s) dell'uscita y(t) fprintf('Output Y(s)'); Y=G*U % Passo 9: scomposizione in fratti semplici di Y(s) [numY,denY]=tfdata(Y,'v'); [residui,poli,resto]=residue(numY,denY)
Input U(s)
U =
1
-
s
Continuous-time transfer function.
U_ =
1
-
s
Continuous-time transfer function.
Output Y(s)
Y =
5 s + 100
-------------------
s^3 + 20 s^2 + 10 s
Continuous-time transfer function.
residui =
0.0069
-10.0069
10.0000
poli =
-19.4868
-0.5132
0
resto =
[]