Esercitazione di laboratorio #2 - Controlli Automatici
Simulazione di risposte di sistemi del I e del II ordine
Autori: M. Indri, M. Taragna (ultima modifica: 22/04/2020)
Contents
Introduzione
Si puo' suddividere il programma in diverse sezioni di codice usando i caratteri "%%". Ogni sezione puo' essere eseguita separatamente dalle altre con il comando "Run Section" (nella toolbar dell'Editor, subito a destra del tasto "Run"). Si puo' ottenere lo stesso risultato selezionando la porzione di codice che si vuole eseguire e premendo il tasto funzione F9, risparmiando cosi' tempo rispetto all'esecuzione di tutto il programma. Si prenda questo script come esempio di riferimento.
clear all, close all, clc
Risposte di sistemi del primo ordine a ingressi canonici
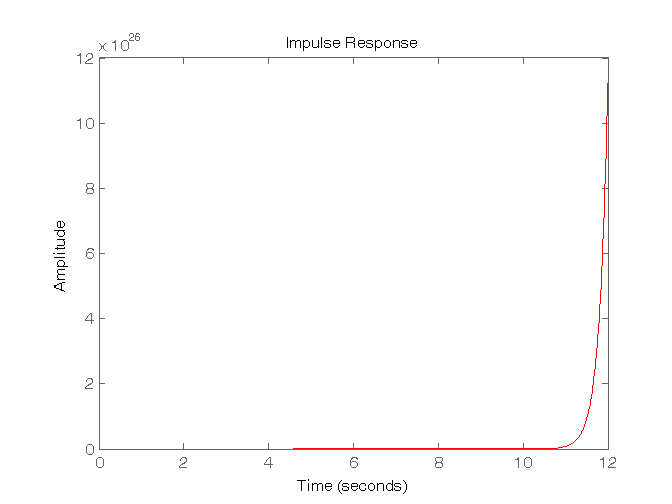
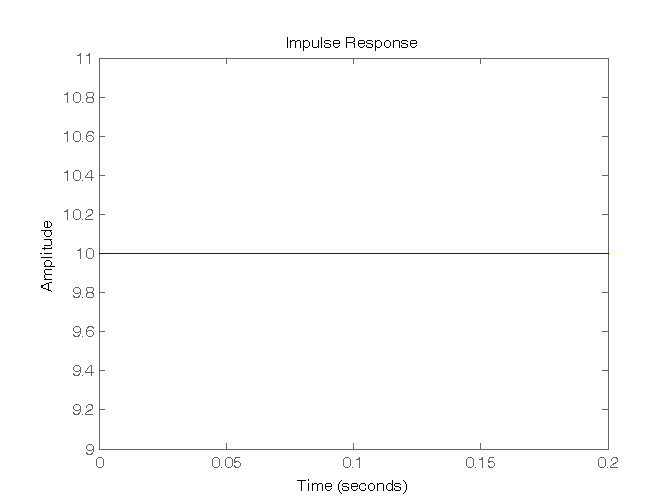
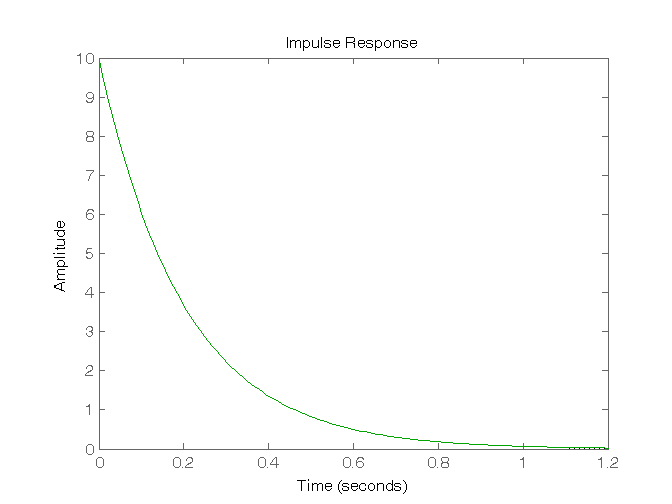
s = tf('s'); % Per definire la variabile “s” G1 = 10/(s-5); G2 = 10/(s+0); G3 = 10/(s+5); G4 = 10/(s+20); % Simulazione della risposta all'impulso figure, impulse(G1,'r'), figure, impulse(G2,'b'), figure, impulse(G3,'g'), figure, impulse(G4,'y'), % Simulazione della risposta al gradino figure, step(G1,'r'), figure, step(G2,'b'), figure, step(G3,'g'), figure, step(G4,'y') pause
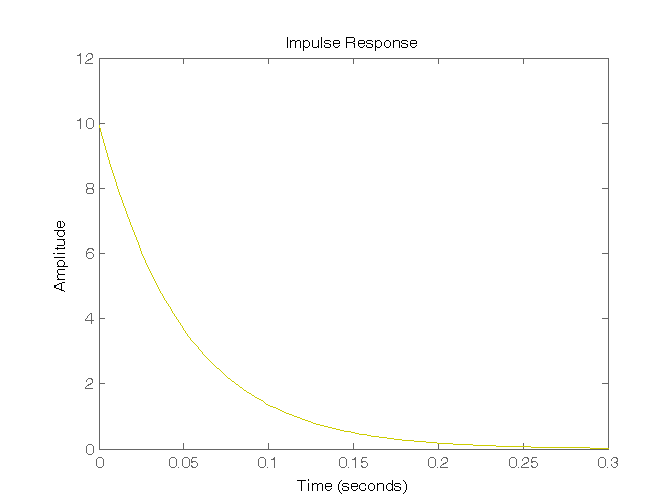
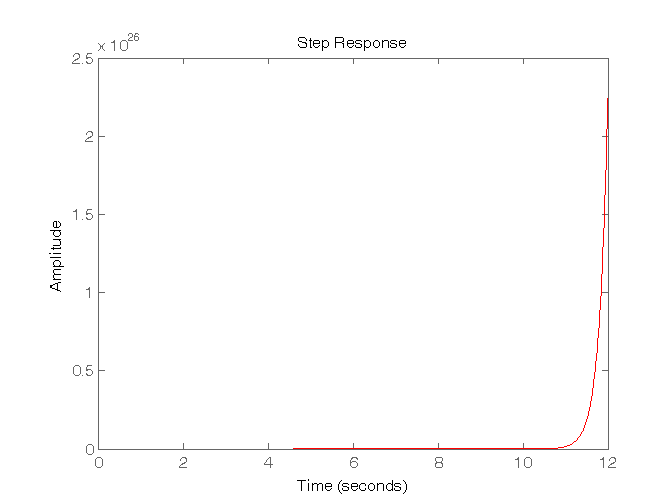
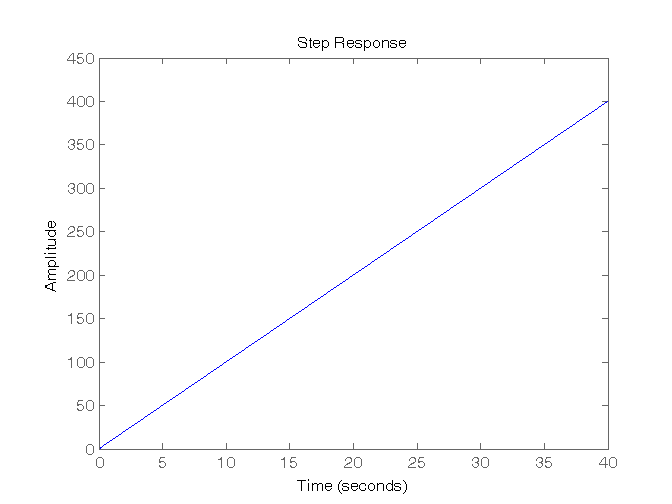
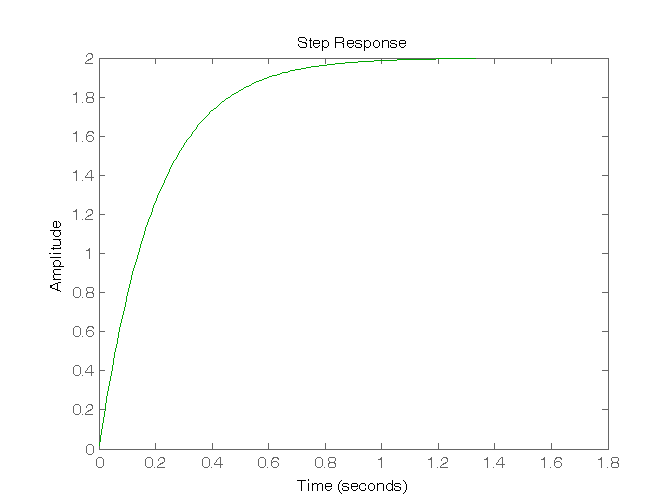
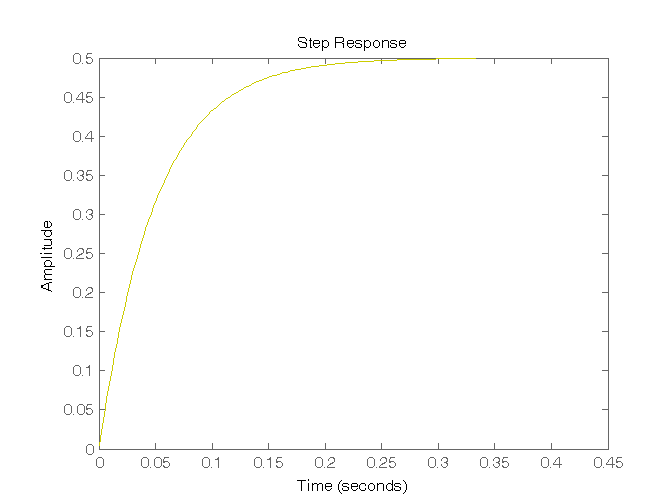
Risposta al gradino di sistemi del II ordine con due poli reali e nessuno zero
s = tf('s'); % Per definire la variabile “s” G1 = 20/((s+1)*(s+10)); G2 = 2/((s+1)^2); G3 = 0.2/((s+1)*(s+0.1)); figure, step(G1,'r', G2,'b', G3,'y'),grid on,
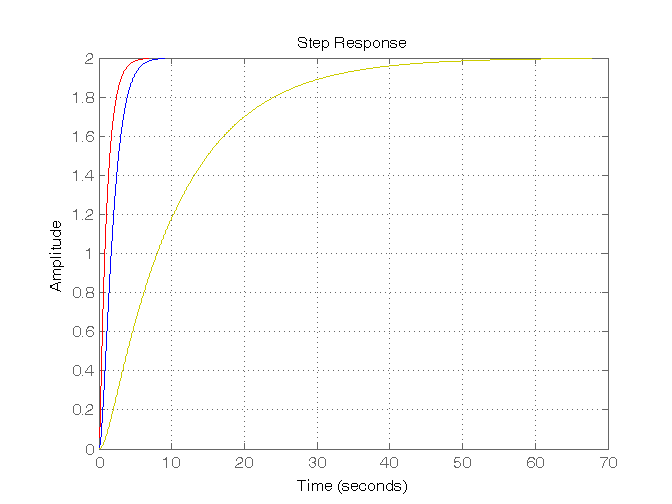
Risposta al gradino di sistemi del II ordine con due poli reali e uno zero
z1 = 100; z2 = 10; z3 = 1; z4 = 0.5; G41 = (5*(s-z1)) / ((-z1)*(s+1)*(s+5)); G42 = (5*(s-z2)) / ((-z2)*(s+1)*(s+5)); G43 = (5*(s-z3)) / ((-z3)*(s+1)*(s+5)); G44 = (5*(s-z4)) / ((-z4)*(s+1)*(s+5)); figure, step(G41,'r', G42,'g', G43,'b', G44,'y'), grid on, %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% z5 = -0.9; z6 = -0.5; z7 = -0.1; G45 = (5*(s-z5)) / ((-z5)*(s+1)*(s+5)); G46 = (5*(s-z6)) / ((-z6)*(s+1)*(s+5)); G47 = (5*(s-z7)) / ((-z7)*(s+1)*(s+5)); figure, step(G45,'r', G46,'b', G47,'g'), grid on, %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% z8 = -100; z9 = -10; z10 = -2; G48 = (5*(s-z8)) / ((-z8)*(s+1)*(s+5)); G49 = (5*(s-z9)) / ((-z9)*(s+1)*(s+5)); G410 = (5*(s-z10)) / ((-z10)*(s+1)*(s+5)); figure, step(G48,'r', G49,'b', G410,'g'),grid on,
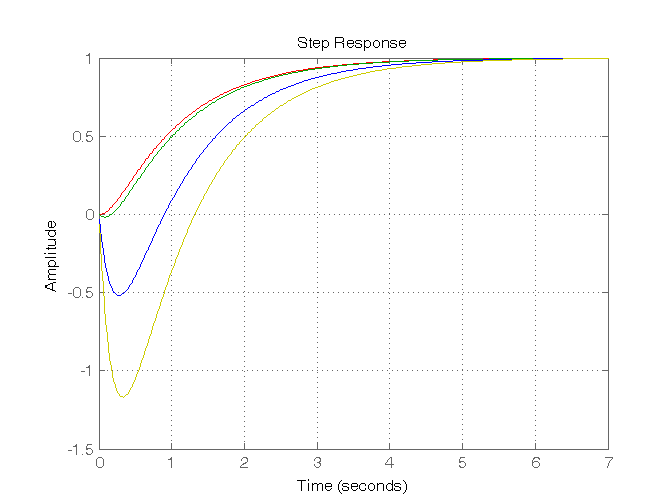
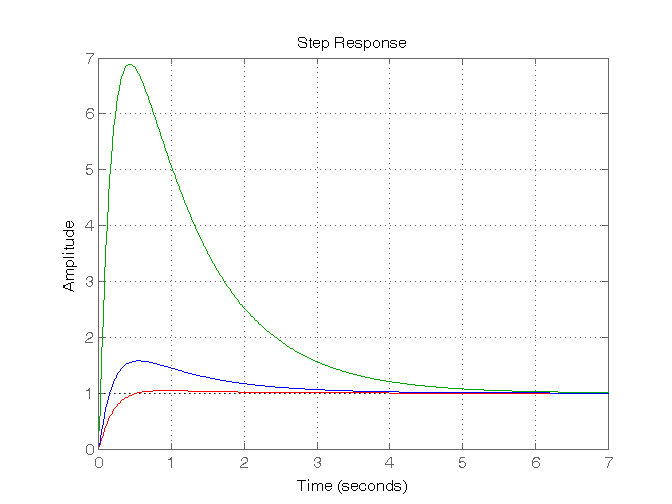
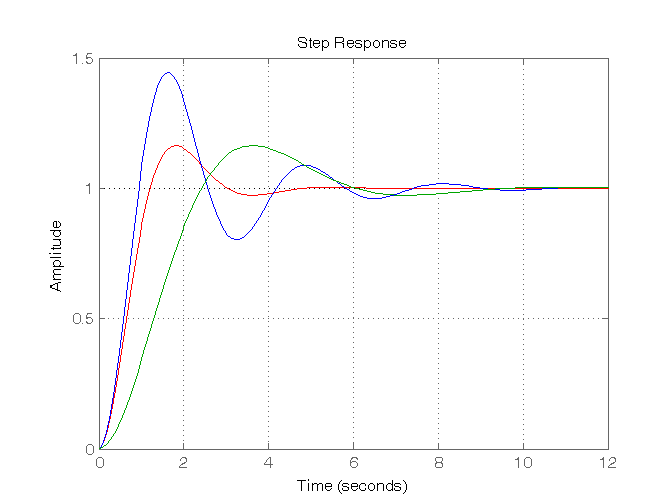
Risposta al gradino di sistemi del II ordine con due poli complessi coniugati
w1 = 2; sigma1 = 0.5; sigma2 = 0.25; w2 = 1; G51 = (w1^2)/((s^2)+(2*sigma1*w1*s)+(w1^2)); G52 = (w1^2)/((s^2)+(2*sigma2*w1*s)+(w1^2)); G53 = (w2^2)/((s^2)+(2*sigma1*w2*s)+(w2^2)); figure, step(G51,'r', G52,'b', G53,'g'),grid on, % Calcolo della sovraelongazione se1 = exp(-pi*sigma1/sqrt(1-sigma1^2)) se2 = exp(-pi*sigma2/sqrt(1-sigma2^2)) se3 = exp(-pi*sigma1/sqrt(1-sigma1^2)) % Calcolo del tempo di salita a = (sqrt(1-sigma1^2))/sigma1; b = (sqrt(1-sigma2^2))/sigma2; ts1 = (1/(w1*sqrt(1-sigma1^2)))*(pi-atan(a)) ts2 = (1/(w1*sqrt(1-sigma2^2)))*(pi-atan(b)) ts3 = (1/(w2*sqrt(1-sigma1^2)))*(pi-atan(a))
se1 =
0.1630
se2 =
0.4443
se3 =
0.1630
ts1 =
1.2092
ts2 =
0.9416
ts3 =
2.4184