Esercitazione di laboratorio #3 - Controlli Automatici

Esercizio #1: progetto del controllo di un levitatore magnetico mediante retroazione statica dallo stato

Autori: M. Indri, M. Taragna (ultima modifica: 28/04/2020)

Contents

Introduzione

Si puo' suddividere il programma in diverse sezioni di codice usando i caratteri "%%". Ogni sezione puo' essere eseguita separatamente dalle altre con il comando "Run Section" (nella toolbar dell'Editor, subito a destra del tasto "Run"). Si puo' ottenere lo stesso risultato selezionando la porzione di codice che si vuole eseguire e premendo il tasto funzione F9, risparmiando cosi' tempo rispetto all'esecuzione di tutto il programma. Si prenda questo script come esempio di riferimento.

clear all, close all, clc

Passo 0: definizione del sistema da controllare (levitatore magnetico)

A=[0, 1; 900, 0];
B=[0; -9];
C=[600, 0];
D=0;

eig_A=eig(A) % Il modello linearizzato e' instabile

eig_A =
   30.0000
  -30.0000

Passo 1: verifica della completa raggiungibilita' del sistema da controllare

Mr=ctrb(A,B)
rank_Mr=rank(Mr)

Mr =
     0    -9
    -9     0
rank_Mr =
     2

Passo 2: assegnazione degli autovalori mediante retroazione statica dallo stato

l1=-40;
l2=-60;
K=place(A,B,[l1,l2])      % In alternativa: acker(A,B,[l1,l2])
eig_A_minus_BK=eig(A-B*K) % Verifica della corretta assegnazione degli autovalori

% Scelta del guadagno alfa

alfa=-1

% Per imporre la condizione di regolazione dell'uscita, basta scommentare:
% alfa=inv(-(C-D*K)*inv(A-B*K)*B+D)

K =
 -366.6667  -11.1111
eig_A_minus_BK =
  -40.0000
  -60.0000
alfa =
    -1

Passo 3: definizione del sistema controllato mediante retroazione dallo stato

Ars=A-B*K
Brs=alfa*B
Crs=C-D*K
Drs=alfa*D

Ars =
   1.0e+03 *
         0    0.0010
   -2.4000   -0.1000
Brs =
     0
     9
Crs =
   600     0
Drs =
     0

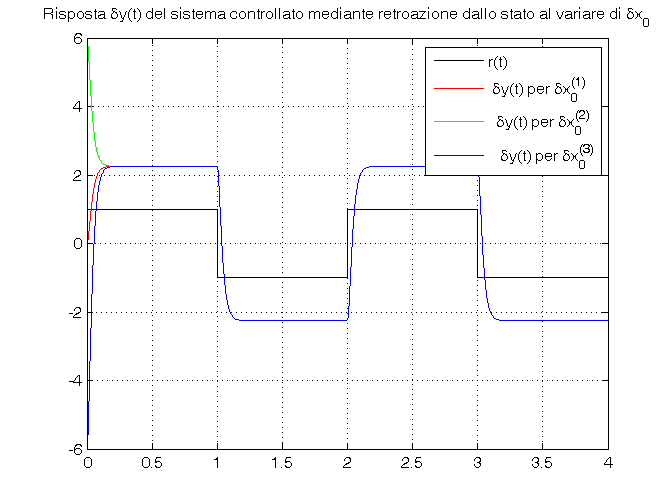
Passo 4: simulazione del sistema controllato mediante retroazione dallo stato

sistema_retroazionato=ss(Ars,Brs,Crs,Drs);
t_r=0:.001:4;
r=sign(sin(2*pi*0.5*t_r));
dx0_1=[ 0.00; 0];
dx0_2=[+0.01; 0];
dx0_3=[-0.01; 0];
[dy_1,t_dy_1]=lsim(sistema_retroazionato,r,t_r,dx0_1);
[dy_2,t_dy_2]=lsim(sistema_retroazionato,r,t_r,dx0_2);
[dy_3,t_dy_3]=lsim(sistema_retroazionato,r,t_r,dx0_3);

figure, plot(t_r,r,'k',t_dy_1,dy_1,'r',t_dy_2,dy_2,'g',t_dy_3,dy_3,'b'), grid on,
title(['Risposta \deltay(t) del sistema controllato mediante retroazione', ...
       ' dallo stato al variare di \deltax_0']),
legend('r(t)',' \deltay(t) per \deltax_0^{(1)}', ...
              '  \deltay(t) per \deltax_0^{(2)}','   \deltay(t) per \deltax_0^{(3)}')

Published with MATLAB® R2014a