Esercitazione di laboratorio #4 - Controlli Automatici

Esercizio #1: Simulazione di un DC-motor comandato in armatura e controllato in velocita'

Autori: M. Indri, M. Taragna (ultima modifica: 07/05/2020)

Contents

Introduzione

Si puo' suddividere il programma in diverse sezioni di codice usando i caratteri "%%". Ogni sezione puo' essere eseguita separatamente dalle altre con il comando "Run Section" (nella toolbar dell'Editor, subito a destra del tasto "Run"). Si puo' ottenere lo stesso risultato selezionando la porzione di codice che si vuole eseguire e premendo il tasto funzione F9, risparmiando cosi' tempo rispetto all'esecuzione di tutto il programma. Si prenda questo script come esempio di riferimento.

clear all, close all, clc

Passo 0: definizione del sistema DC-motor comandato in armatura

% Parametri del motore elettrico
Ra=1; La=6e-3; Km=0.5; J=0.1; b=0.02; Ka=10;

s=tf('s');
F1=Ka*Km/((s*La+Ra)*(s*J+b)+Km^2)
F2=-(s*La+Ra)/((s*La+Ra)*(s*J+b)+Km^2)

F1 =
 
               5
  ----------------------------
  0.0006 s^2 + 0.1001 s + 0.27
 
Continuous-time transfer function.


F2 =
 
          -0.006 s - 1
  ----------------------------
  0.0006 s^2 + 0.1001 s + 0.27
 
Continuous-time transfer function.

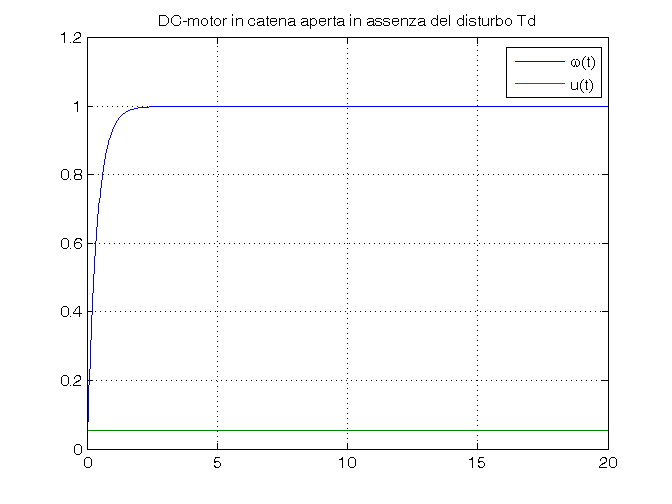
Passo 1: simulazione in catena aperta in assenza del disturbo Td

Td_amp=0

open_system('es_motore_no_controllo_velocita')
sim('es_motore_no_controllo_velocita')
w_rif=1/dcgain(F1)*ones(size(tout));
figure, plot(tout,vel_ang, tout,w_rif), grid on, ylim([0,1.2]),
title('DC-motor in catena aperta in assenza del disturbo Td'),
legend('\omega(t)','u(t)')

Td_amp =
     0

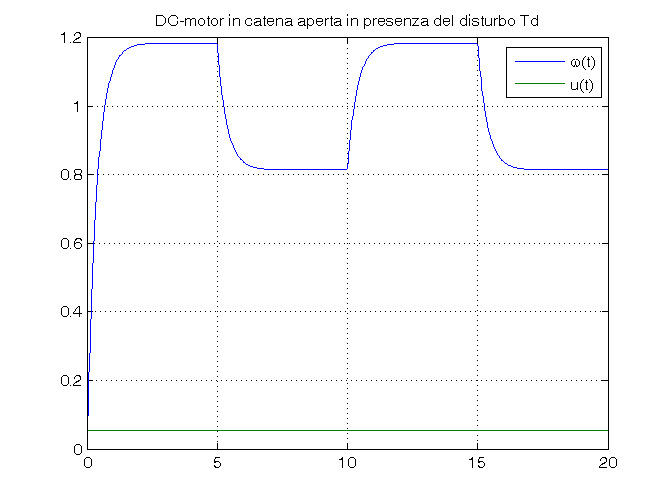
Passo 2: simulazione in catena aperta in presenza del disturbo Td

Td_amp=0.05

sim('es_motore_no_controllo_velocita')
w_rif=1/dcgain(F1)*ones(size(tout));
figure, plot(tout,vel_ang, tout,w_rif), grid on, ylim([0,1.2]),
title('DC-motor in catena aperta in presenza del disturbo Td'),
legend('\omega(t)','u(t)')
close_system('es_motore_no_controllo_velocita')

Td_amp =
    0.0500

Passo 3: simulazione in catena chiusa in assenza del disturbo Td

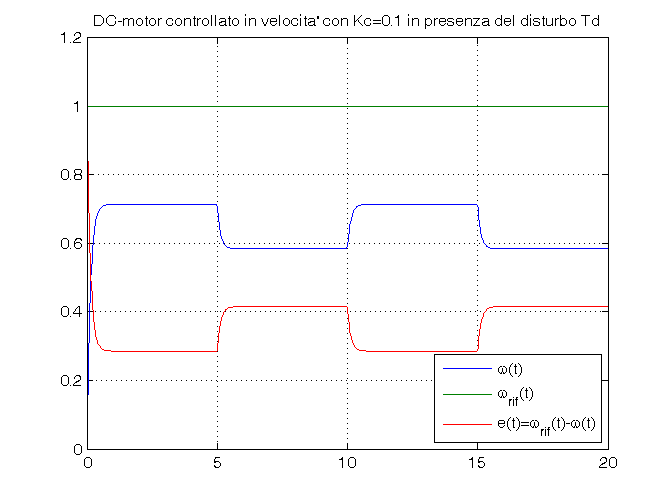
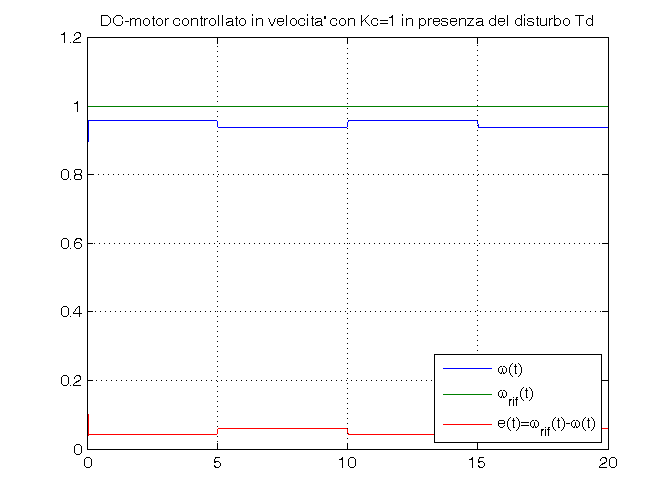
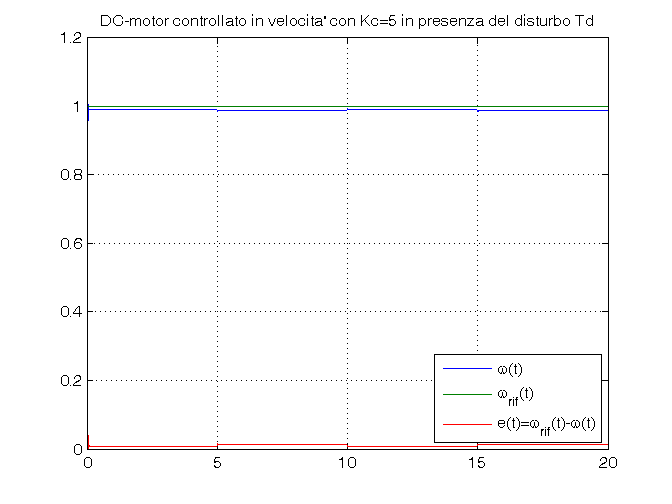
Td_amp=0
Kc_vec=[0.1, 1, 5];

open_system('es_motore_con_controllo_velocita')
for Kc=Kc_vec,
    sim('es_motore_con_controllo_velocita')
    w_rif=ones(size(tout));
    errore=w_rif-vel_ang;
    figure, plot(tout,vel_ang, tout,w_rif, tout,errore), grid on, ylim([0,1.2]),
    title(['DC-motor controllato in velocita'' con Kc=', num2str(Kc), ...
           ' in assenza del disturbo Td']),
    legend('\omega(t)','\omega_{rif}(t)','e(t)=\omega_{rif}(t)-\omega(t)',4)
end

Td_amp =
     0

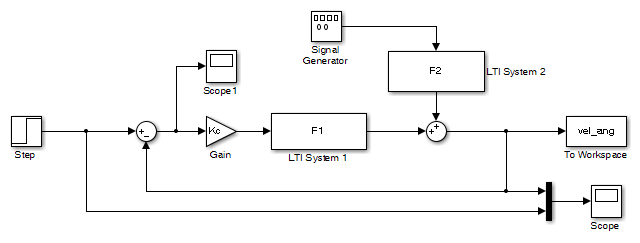
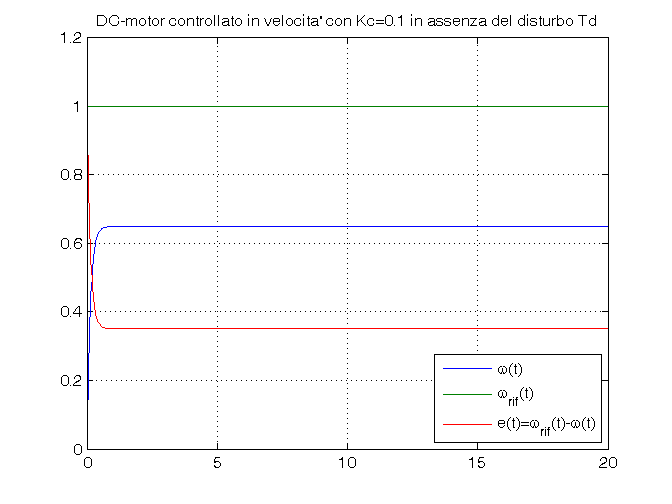
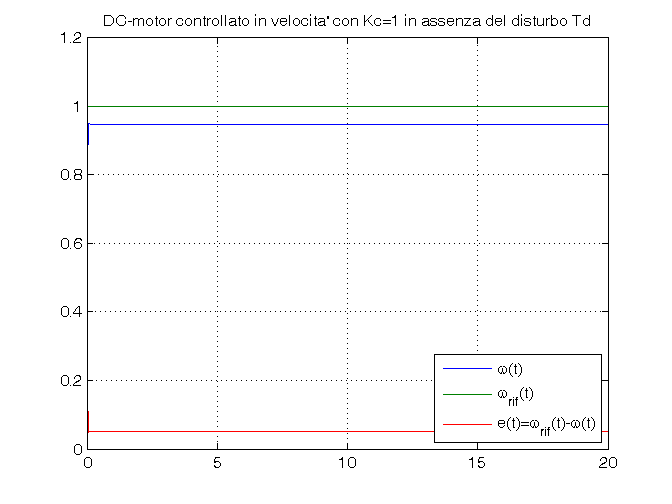
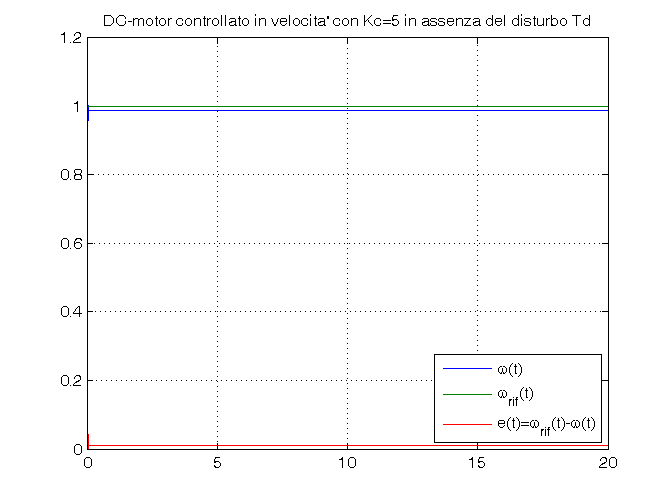
Passo 4: simulazione in catena chiusa in presenza del disturbo Td

Td_amp=0.05

for Kc=Kc_vec,
    sim('es_motore_con_controllo_velocita')
    w_rif=ones(size(tout));
    errore=w_rif-vel_ang;
    figure, plot(tout,vel_ang, tout,w_rif, tout,errore), grid on, ylim([0,1.2]),
    title(['DC-motor controllato in velocita'' con Kc=', num2str(Kc), ...
           ' in presenza del disturbo Td']),
    legend('\omega(t)','\omega_{rif}(t)','e(t)=\omega_{rif}(t)-\omega(t)',4)
end
close_system('es_motore_con_controllo_velocita')

Td_amp =
    0.0500

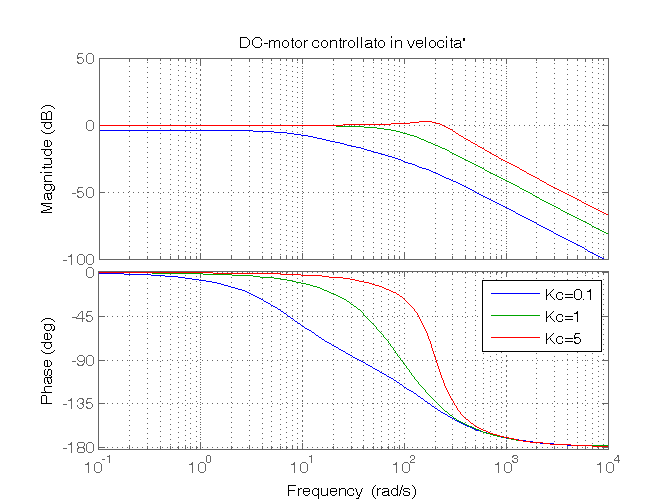
Passo 5: calcolo delle f.d.t. in catena chiusa e dei diagrammi di Bode

figure
for Kc=Kc_vec,
    Kc
    W=feedback(Kc*F1,1)
    z_W=zero(W)
    p_W=pole(W)
    damp(W)
    bode (W), grid on, xlim([1e-1, 1e4]), hold on,
    title('DC-motor controllato in velocita''')
end
legend(['Kc=',num2str(Kc_vec(1))],['Kc=',num2str(Kc_vec(2))],['Kc=',num2str(Kc_vec(3))])

Kc =
    0.1000

W =
 
              0.5
  ----------------------------
  0.0006 s^2 + 0.1001 s + 0.77
 
Continuous-time transfer function.

z_W =
   Empty matrix: 0-by-1
p_W =
 -158.7844
   -8.0822
                                                           
   Pole        Damping       Frequency      Time Constant  
                           (rad/seconds)      (seconds)    
                                                           
 -8.08e+00     1.00e+00       8.08e+00         1.24e-01    
 -1.59e+02     1.00e+00       1.59e+02         6.30e-03    
Kc =
     1

W =
 
               5
  ----------------------------
  0.0006 s^2 + 0.1001 s + 5.27
 
Continuous-time transfer function.

z_W =
   Empty matrix: 0-by-1
p_W =
 -83.4333 +42.6874i
 -83.4333 -42.6874i
                                                                       
         Pole              Damping       Frequency      Time Constant  
                                       (rad/seconds)      (seconds)    
                                                                       
 -8.34e+01 + 4.27e+01i     8.90e-01       9.37e+01         1.20e-02    
 -8.34e+01 - 4.27e+01i     8.90e-01       9.37e+01         1.20e-02    
Kc =
     5

W =
 
               25
  -----------------------------
  0.0006 s^2 + 0.1001 s + 25.27
 
Continuous-time transfer function.

z_W =
   Empty matrix: 0-by-1
p_W =
   1.0e+02 *
  -0.8343 + 1.8750i
  -0.8343 - 1.8750i
                                                                       
         Pole              Damping       Frequency      Time Constant  
                                       (rad/seconds)      (seconds)    
                                                                       
 -8.34e+01 + 1.87e+02i     4.07e-01       2.05e+02         1.20e-02    
 -8.34e+01 - 1.87e+02i     4.07e-01       2.05e+02         1.20e-02    

Published with MATLAB® R2014a