Esercitazione di laboratorio #7 - Controlli Automatici

Esercizio #1

Autori: M. Indri, M. Taragna (ultima modifica: 28/05/2020)

Contents

Comandi di pulizia iniziali

clear all, close all

Definizione del sistema e calcolo del guadagno stazionario

s=tf('s');
F=13.5*(s+4)*(s+10)/(s+3)^3;
KF=dcgain(F)

Kr=1;

KF =

    20

Analisi delle specifiche

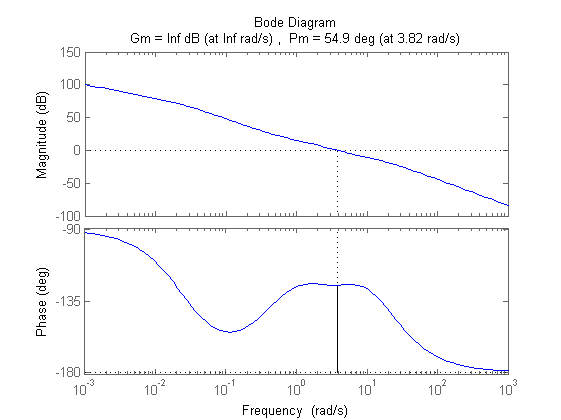
% specifica a) =>
% 1) C(s) con 1 polo nell'origine,
% 2) |Kr/KGa| <= 0.01 => |Kc| >= 100*Kr^2/|KF|   => |Kc| >= 5

% specifica b) e' soddisfatta se C(s) ha 1 polo nell'origine

% segno di Kc positivo: il sistema è a stabilità regolare
bode(F/s)

% specifica c) => wc < B3 < 2*wc => wc ~= 0.63 * B3

wc_des=3.8

% specifica d) => (su Nichols) margine_di_fase >= 45deg => meglio ~50deg

wc_des =

    3.8000

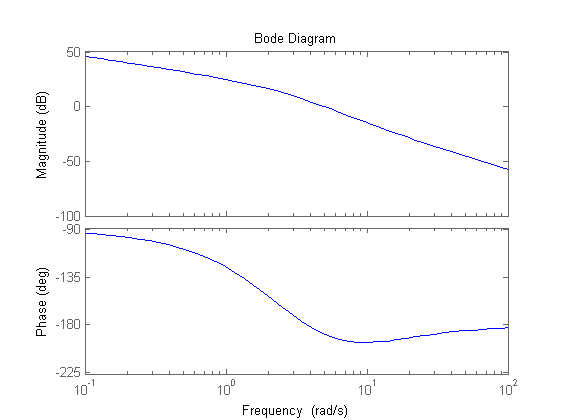
Funzione d'anello di partenza e valutazione azioni da intraprendere

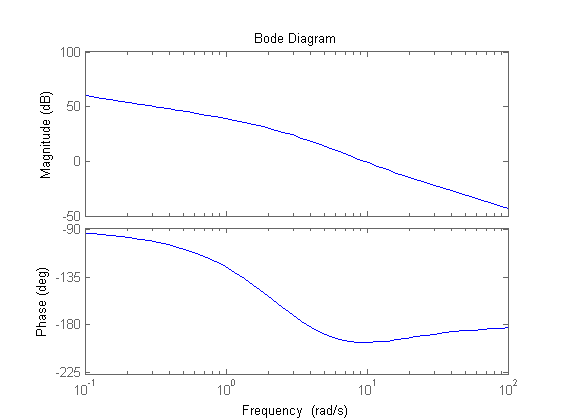
Kc=5 % minimo valore ammissibile
Ga1=(Kc/s)*F/Kr

figure, bode(Ga1)

[m_wc_des,f_wc_des]=bode(Ga1,wc_des)

% In wc_des il modulo vale circa 19.3 dB e la fase -180.8 deg
% Risulta necessario recuperare circa 60 deg prevedendo di dover inserire
% anche una rete attenuatrice per ridurre il modulo.
% Il recupero della fase sarà ottenuto usando due reti derivative.
% Si consiglia di provare a risolvere l'esercizio anche utilizzando uno zero
% reale negativo (fisicamente realizzabile insieme al polo già inserito
% nell'origine) al posto delle reti derivative.

Kc =

     5


Ga1 =
 
    67.5 s^2 + 945 s + 2700
  ---------------------------
  s^4 + 9 s^3 + 27 s^2 + 27 s
 
Continuous-time transfer function.


m_wc_des =

    9.2384


f_wc_des =

 -180.7915

Progetto delle reti di compensazione

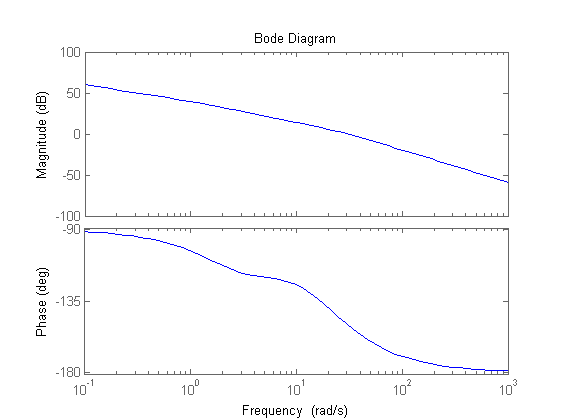
% Inserimento di due reti derivative uguali da 4 per recuperare 60deg in w=wc_des,
% progettate sul fronte di salita del recupero di fase in xd = 1 per limitare l'aumento di modulo
% ed evitare la successiva necessità di una rete attenuatrice molto forte

m_a=4
xd=1
tau_a=xd/wc_des
Rd=(1+tau_a*s)/(1+tau_a/m_a*s)

[m1_wc_des,f1_wc_des]=bode(Rd^2*Ga1,wc_des)
figure, bode(Rd^2*Ga1)

% Inserimento di una rete integrativa con m_i=m1_wc_des ~= 17.4 per avere wc_finale=wc_des
% e progettata in xi=150 per perdere meno di 10 gradi di fase in w=wc_des
% (vedere i diagrammi di Bode normalizzati della rete tracciati in Matlab)

m_i=17.4
figure,bode((1+s/m_i)/(1+s))
xi=150
tau_i=xi/wc_des
Ri=(1+tau_i/m_i*s)/(1+tau_i*s)

m_a =

     4


xd =

     1


tau_a =

    0.2632


Rd =
 
  0.2632 s + 1
  -------------
  0.06579 s + 1
 
Continuous-time transfer function.


m1_wc_des =

   17.3899


f1_wc_des =

 -118.8640


m_i =

   17.4000


xi =

   150


tau_i =

   39.4737


Ri =
 
  2.269 s + 1
  -----------
  39.47 s + 1
 
Continuous-time transfer function.

Verifica del soddisfacimento dei requisiti su Ga e definizione del controllore

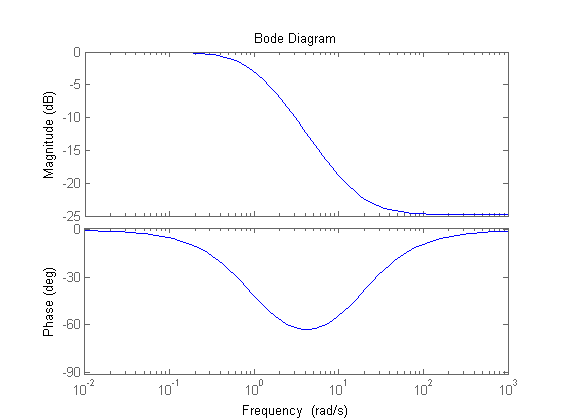
figure, margin(Rd^2*Ri*Ga1)

C=Kc/s*Rd^2*Ri
Ga=C*F/Kr;

C =
 
   0.7855 s^3 + 6.316 s^2 + 13.97 s + 5
  --------------------------------------
  0.1709 s^4 + 5.198 s^3 + 39.61 s^2 + s
 
Continuous-time transfer function.

Verifica delle specifiche in catena chiusa

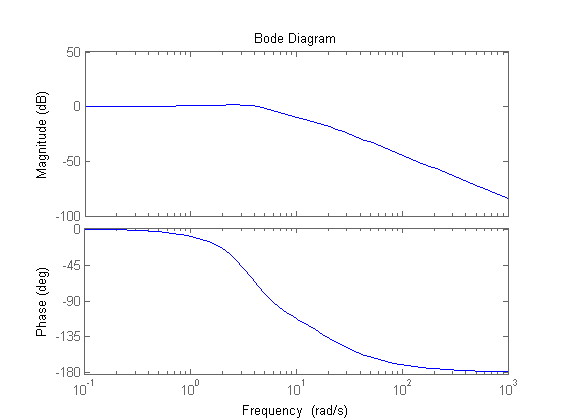
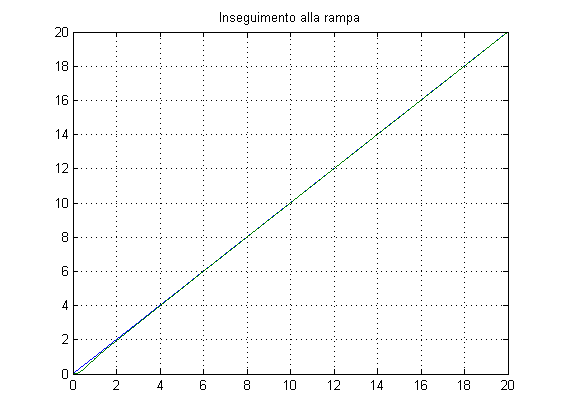
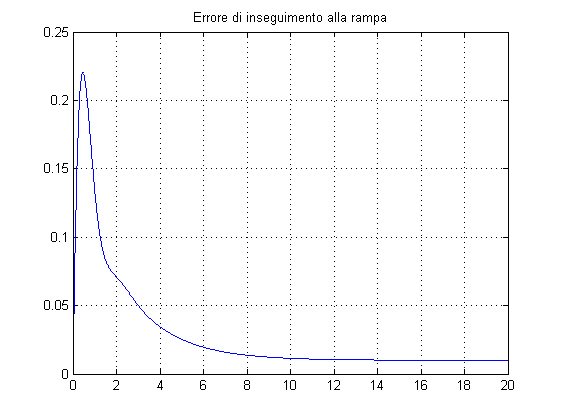
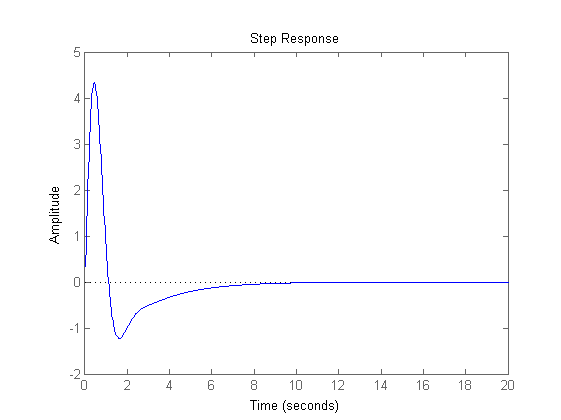
% Verifica della banda passante e del picco di risonanza
% (si ottiene wB = 5.7 rad/s, Mr = 1.7 dB <2 dB)
W=feedback(C*F,1/Kr);
figure, bode(W)

% Verifica dell'errore di inseguimento alla rampa
% (si ottiene errore = 0.01 in regime permanente)
t=0:0.01:20;
r=t';
y_rampa=lsim(W,r,t);
figure, plot(t,r,t,y_rampa), title('Inseguimento alla rampa'), grid on
figure, plot(t,Kr*r-y_rampa), title('Errore di inseguimento alla rampa'), grid on

% Verifica dell'effetto (nullo) del disturbo (astaticità)
Wd=feedback(F,1/Kr*C);
figure, step(Wd,20)

Valutazione delle prestazioni in catena chiusa

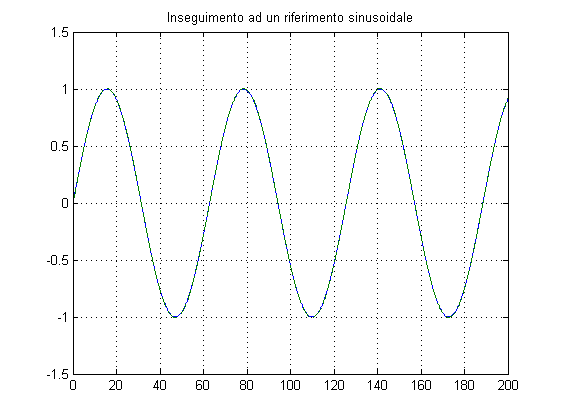
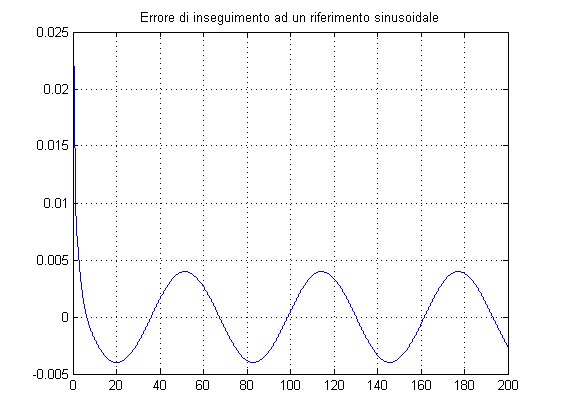
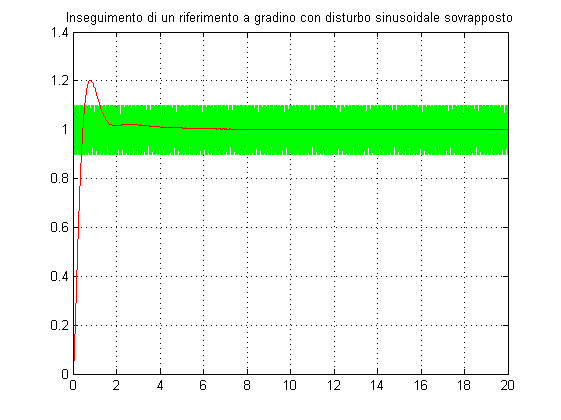
% Calcolo dell'errore di inseguimento in regime permanente
% a riferimento sinusoidale sin(0.1*t)
w_r=0.1;
Sens=feedback(1,Ga);
errore_sin=bode(Sens,w_r)*Kr

% Verifica dell'errore di inseguimento in regime permanente
% a riferimento sinusoidale sin(0.1*t)
t=0:0.01:200;
r=sin(w_r*t)';
y=lsim(W,r,t);
figure, plot(t,r,t,y,'--'), title('Inseguimento ad un riferimento sinusoidale'), grid on
figure, plot(t,Kr*r-y), title('Errore di inseguimento ad un riferimento sinusoidale'), grid on

% Attenuazione di disturbi sinusoidali entranti sul riferimento,
% aventi pulsazione=100rad/s
w_disturbi_r=100;
attenuazione_disturbi_r=bode(W,w_disturbi_r)

% Verifica dell'attenuazione di disturbi sinusoidali entranti insieme
% al riferimento a gradino unitario, nel caso che tali disturbi abbiano
% ampiezza=0.1, pulsazione=100rad/s
% Nel grafico: in rosso la rispotsa del sistema, in verde il riferimento a
% soggetto al disturbo

t=0:0.001:20;
r_disturbato=ones(size(t))+0.1*sin(w_disturbi_r*t);
y_r_disturbato=lsim(W,r_disturbato,t);
figure, plot(t,r_disturbato,'g',t,y_r_disturbato,'r'), grid on,
title('Inseguimento di un riferimento a gradino con disturbo sinusoidale sovrapposto')

errore_sin =

    0.0040


attenuazione_disturbi_r =

    0.0061

Nota finale

% In questa soluzione proposta tutte le simulazioni sono state eseguite
% utilizzando soltanto Matlab al fine di avere un unico file comprensivo di tutte le parti.
% Gli studenti sono invitati a costruire il corrispondente schema Simulink
% ed a svolgere con esso le verifiche delle specifiche e le valutazioni
% richieste in catena chiusa.

Published with MATLAB® R2014a