Esercitazione di laboratorio #7 - Controlli Automatici

Esercizio #2

Autori: M. Indri, M. Taragna (ultima modifica: 28/05/2020)

Contents

Comandi di pulizia iniziali

clear all, close all

Definizione del sistema e calcolo del guadagno stazionario

s=tf('s');
F=5*(s+20)/(s*(s^2+2.5*s+2)*(s^2+15*s+100));
KF=dcgain(s*F)

Kr=2;

KF =

    0.5000

Analisi delle specifiche

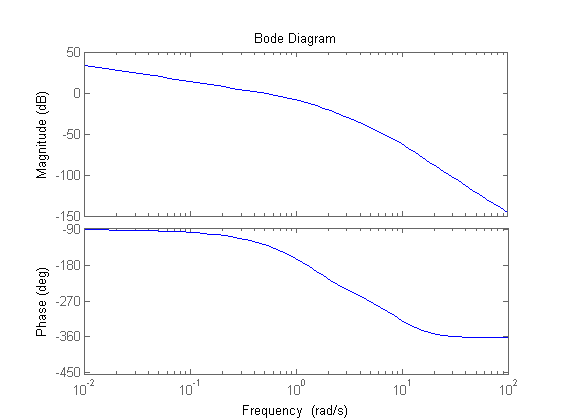
% specifica a) =>
% 1) non richiede inserimento di poli nell'origine (ce n'e' gia' uno in F(s))
% 2) |Kr/KGa| <= 0.05 => |Kc| >= 20*Kr^2/|KF|   => |Kc| >= 160

% specifica b) =>
% 1) non richiede inserimento di poli nell'origine (il disturbo è costante)
% 2) |d/(Kc/Kr)|<= 0.02 => |Kr/Kc|<=0.02 => |Kc|>=100

% segno di Kc positivo: il sistema è a stabilità regolare
bode(F)

% specifica c) => ts = 1s => B3 ~=3/ts =3 =>
% wc < B3 < 2*wc => wc ~= 0.63*B3

wc_des=1.9

% specifica d) => s_hat=0.3 => Mr <= 1.44, Mr_dB=3.2dB
% (su Nichols) margine_di_fase >= 40deg => meglio 45deg

wc_des =

    1.9000

Funzione d'anello di partenza e valutazione azioni da intraprendere

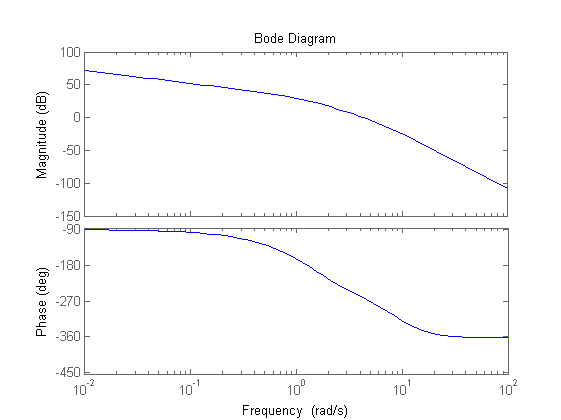
Kc=160 % minimo valore ammissibile
Ga1=Kc*F/Kr

figure, bode(Ga1)

[m_wc_des,f_wc_des]=bode(Ga1,wc_des)

% In wc_des il modulo vale circa 18.5 dB e la fase -209.8 deg
% Risulta necessario recuperare circa 80 deg prevedendo di dover inserire
% anche una rete attenuatrice per ridurre il modulo.
% Il recupero della fase dovrà essere ottenuto usando due reti derivative.

Kc =

   160


Ga1 =
 
                800 s + 16000
  ------------------------------------------
  2 s^5 + 35 s^4 + 279 s^3 + 560 s^2 + 400 s
 
Continuous-time transfer function.


m_wc_des =

    8.3897


f_wc_des =

 -209.7687

Progetto delle reti di compensazione

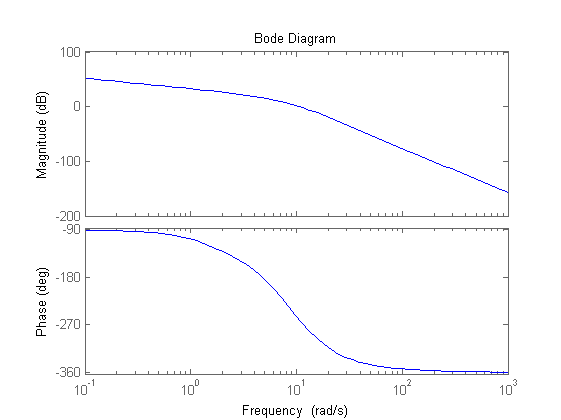
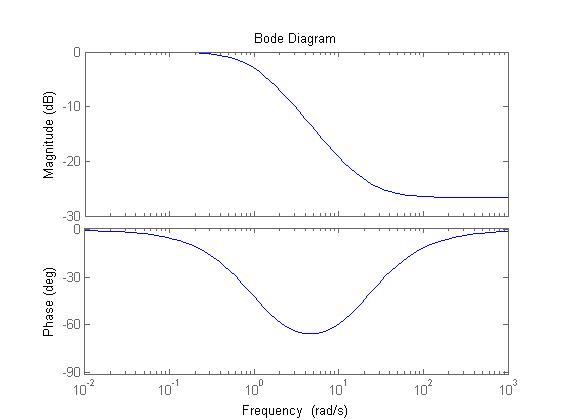
% Inserimento di due reti derivative uguali da 6 per recuperare 80deg in w=wc_des,
% progettate sul fronte di salita del recupero di fase in xd = 1.3 per limitare l'aumento di modulo
% ed evitare la successiva necessità di una rete attenuatrice molto forte

m_a=6
xd=1.3
tau_a=xd/wc_des
Rd=(1+s*tau_a)/(1+s*tau_a/m_a)

[m1_wc_des,f1_wc_des]=bode(Rd^2*Ga1,wc_des)
figure, bode(Rd^2*Ga1)

% Inserimento di una rete integrativa con m_i=m1_wc_des ~= 21.5 per avere wc_finale=wc_des
% e progettata in xi=230 per perdere circa 5 gradi di fase in w=wc_des
% (vedere i diagrammi di Bode normalizzati della rete tracciati in Matlab)

m_i=21.5
figure,bode((1+s/m_i)/(1+s))
xi=230
tau_i=xi/wc_des
Ri=(1+s*tau_i/m_i)/(1+s*tau_i)

m_a =

     6


xd =

    1.3000


tau_a =

    0.6842


Rd =
 
  4.105 s + 6
  ------------
  0.6842 s + 6
 
Continuous-time transfer function.


m1_wc_des =

   21.5564


f1_wc_des =

 -129.3561


m_i =

   21.5000


xi =

   230


tau_i =

  121.0526


Ri =
 
  121.1 s + 21.5
  --------------
  2603 s + 21.5
 
Continuous-time transfer function.

Verifica del soddisfacimento dei requisiti su Ga e definizione del controllore

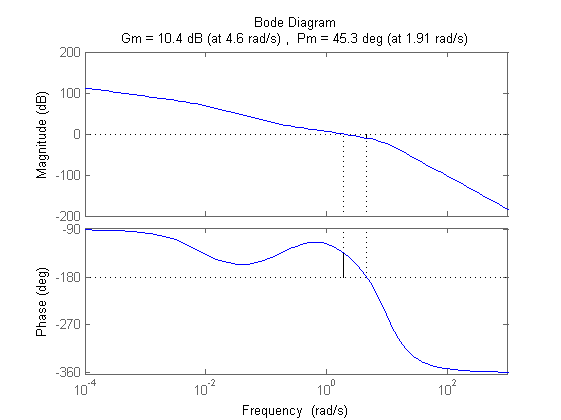
figure, margin(Rd^2*Ri*Ga1)

C=Kc*Rd^2*Ri
Ga=C*F/Kr;

C =
 
  3.264e05 s^3 + 1.012e06 s^2 + 8.667e05 s + 123840
  -------------------------------------------------
     1218 s^3 + 2.138e04 s^2 + 9.387e04 s + 774
 
Continuous-time transfer function.

Verifica delle specifiche in catena chiusa

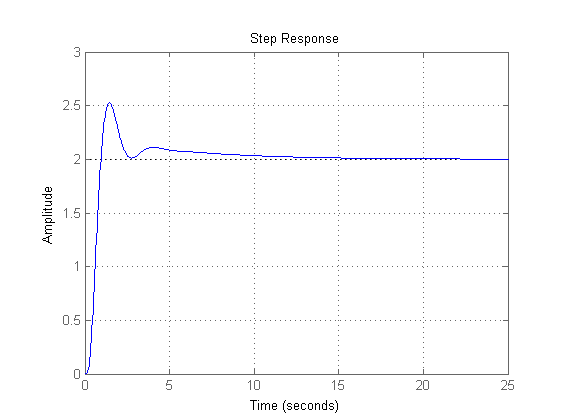
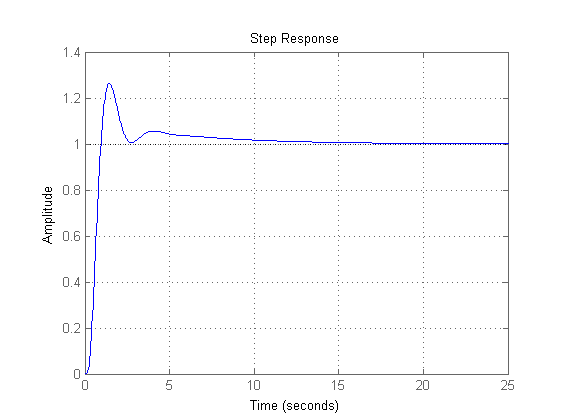
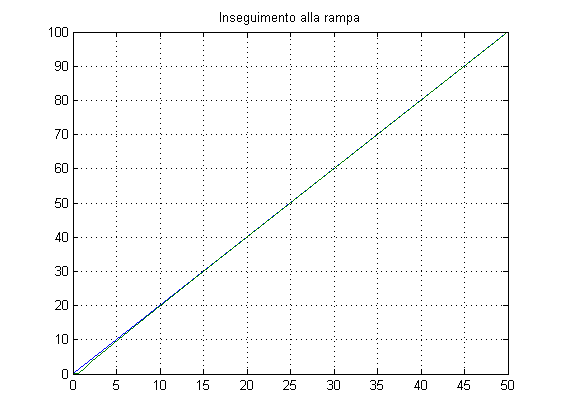
W=feedback(C*F,1/Kr);

% Verifica delle specifiche sulla risposta al gradino t_s e s_hat
% La divisione per Kr permette di valutare direttamente s_hat=0.263 dal
% valore massimo; il tempo salita risulta pari a 0.94 s
% (confrontare il risultato dai due grafici!)

figure, step(W), grid on
figure, step(W/Kr), grid on

% Verifica dell'errore di inseguimento alla rampa
% (si ottiene errore = 0.05 in regime permanente)
t=0:0.01:50;
r=t';
y_rampa=lsim(W,r,t);
figure, plot(t,Kr*r,t,y_rampa), title('Inseguimento alla rampa'), grid on
figure, plot(t,Kr*r-y_rampa), title('Errore di inseguimento alla rampa'), grid on

% Verifica dell'effetto del disturbo in regime permanente (pari a 0.0125)
Wd=feedback(F,1/Kr*C);
figure, step(Wd,50)

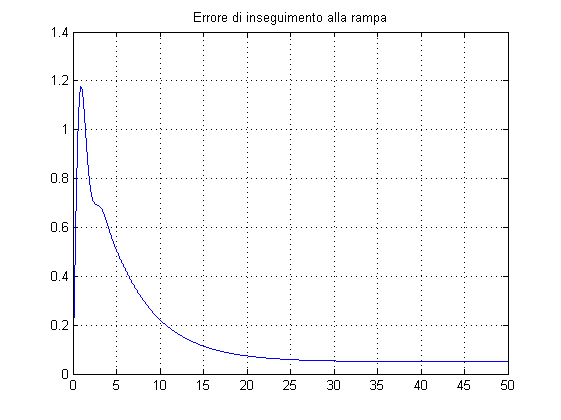
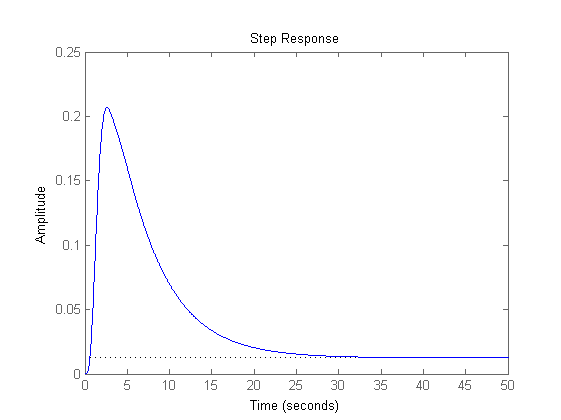
Valutazione delle prestazioni in catena chiusa

% Attività sul comando:
% confrontare il valore iniziale del grafico con quanto ricavabile dal
% teorema del valore iniziale; si ottiene u(o)=Kc*m_a^2/m_i = 267.9...

Wu=feedback(C,F/Kr);
figure,step(Wu)

% Valutazione banda passante e picco di risonanza
% La divisione per Kr permette di valutare direttamente B3 e Mr
% Confrontare i risultati dai due grafici: Mr=2.3 dB, B3=3.65 rad/s

figure,bode(W)
figure, bode(W/Kr)

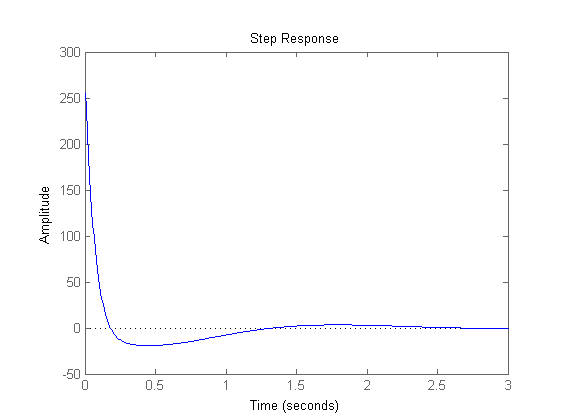
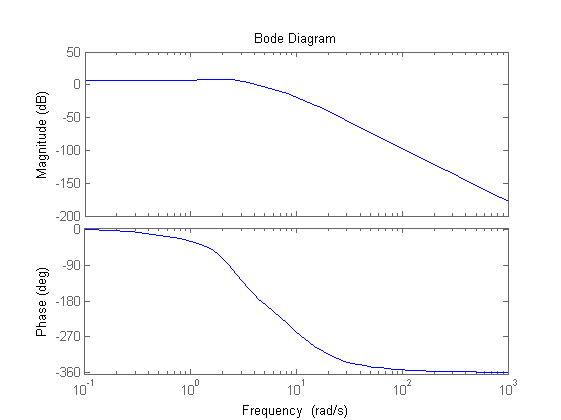
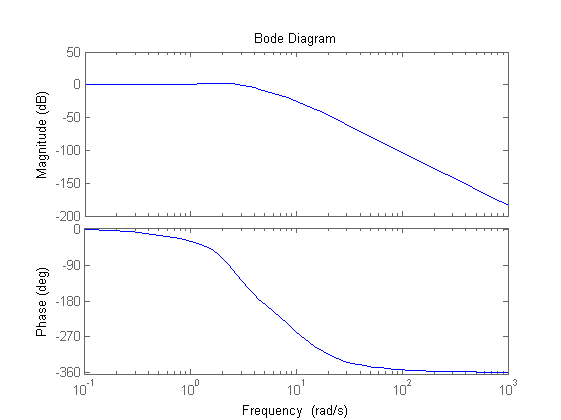
Confronto con una soluzione alternativa

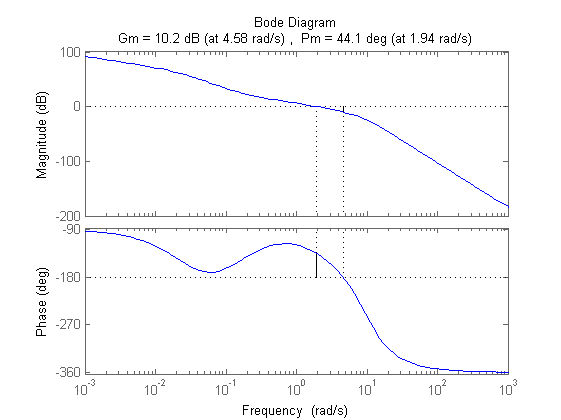
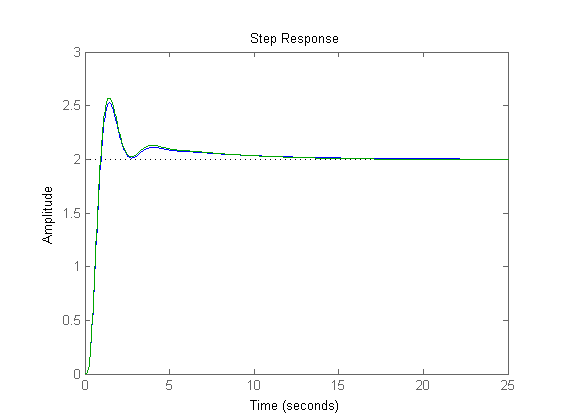
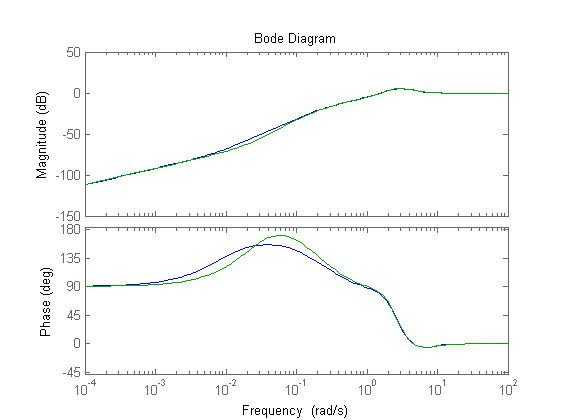
% Soluzione alternativa: reti derivative invariate, utilizzo di 2 attenuatrici meno forti
% da 4.6 progettate in xi_alt = 70

m_i_alt=4.6
xi_alt=70
tau_i_alt=xi_alt/wc_des
Ri_alt=(1+s*tau_i_alt/m_i_alt)/(1+s*tau_i_alt)

C_alt=Kc*Rd^2*Ri_alt^2;
Ga_alt=C_alt*F/Kr;
figure,margin(Ga_alt)

% Confronti ad anello chiuso delle due soluzioni:
% la prima soluzione è complessivamente migliore perché
% (1) corrisponde ad un controllore di ordine minore (ho usato una rete in meno)
% (2) presenta un effetto coda leggermente ridotto (grafico blu)
% la seconda soluzione ha come unico vantaggio una sensibilità ridotta
% per w comprese fra 0.007 e 0.1

Sens=feedback(1,Ga); % sensibilità per la soluzione originale

W_alt=feedback(C_alt*F,1/Kr);
figure,step(W)
hold
step(W_alt)
hold off
Sens_alt=feedback(1,Ga_alt);
figure,bode(Sens)
hold
bode(Sens_alt)
hold off

m_i_alt =

    4.6000


xi_alt =

    70


tau_i_alt =

   36.8421


Ri_alt =
 
  36.84 s + 4.6
  -------------
  169.5 s + 4.6
 
Continuous-time transfer function.

Current plot held
Current plot held

Nota finale

% In questa soluzione proposta tutte le simulazioni sono state eseguite
% utilizzando soltanto Matlab al fine di avere un unico file di tutte le parti.
% Gli studenti sono invitati a costruire il corrispondente schema Simulink
% ed a svolgere con esso le verifiche delle specifiche e le valutazioni
% richieste in catena chiusa.

Published with MATLAB® R2014a